DeblurSDI: blind image deblurring using self-diffusion

TLDR We propose DeblurSDI using self-diffusion, a zero-shot, self-supervised framework that requires no prior training.

Abstract Blind image deconvolution is a challenging ill-posed inverse problem, where both the latent sharp image and the blur kernel are unknown. Traditional methods often rely on handcrafted priors, while modern deep learning approaches typically require extensive pre-training on large external datasets, limiting their adaptability to real-world scenarios. In this work, we propose DeblurSDI, a zero-shot, self-supervised framework based on self-diffusion (SDI) that requires no prior training. DeblurSDI formulates blind deconvolution as an iterative reverse self-diffusion process that starts from pure noise and progressively refines the solution. At each step, two randomly-initialized neural networks are optimized continuously to refine the sharp image and the blur kernel. The optimization is guided by an objective function combining data consistency with a sparsity-promoting -norm for the kernel. A key innovation is our noise scheduling mechanism, which stabilizes the optimization and provides remarkable robustness to variations in blur kernel size. These allow DeblurSDI to dynamically learn an instance-specific prior tailored to the input image. Extensive experiments demonstrate that DeblurSDI consistently achieves superior performance, recovering sharp images and accurate kernels even in highly degraded scenarios.

Methods The forward model for blind image deblurring is given by

\begin{equation} \mathbf{y} = \mathbf{x}_\text{true} \circledast \mathbf{k} + n~, \end{equation}

where the sharp image \(\mathbf{x}_\text{true} \in \mathbb{R}^{H \times W \times C}\) and the blur kernel \(\mathbf{k} \in \mathbb{R}^{K \times K}\) are both unknown. To adapt the self-diffusion framework to this blind setting, we must estimate both variables simultaneously. We achieve this by employing two dedicated, randomly initialized networks: an image denoiser \(D_\theta\) to restore \(\mathbf{x}_\text{true}\), and a kernel generator \(G_\phi\) to produce \(\mathbf{k}\). Our method simulates a reverse diffusion process over \(T\) discrete time steps, starting with random noise for both the image estimate, \(\mathbf{x}_T\), and the kernel estimate, \(\mathbf{z}_T\). At each time step \(t \in \{T, T-1, ..., 1\}\), the current estimates are perturbed with scheduled noise,

\begin{equation} \hat{\mathbf{x}}_t = \mathbf{x}_t + \sigma_t \cdot \epsilon_x, \quad \text{and} \quad \hat{\mathbf{z}}_t = \mathbf{z}_t + \sigma’_t \cdot \epsilon_z, \end{equation}

where \(\epsilon_x \sim \mathcal{N}(0, \mathbf{I})\) and \(\epsilon_z \sim \mathcal{N}(0, \mathbf{I})\). The noise schedule is \(\sigma_t = \sqrt{1 - \bar{\alpha}_t}\), where \(\bar{\alpha}_t = \mathop{\textstyle\prod}\nolimits_{i=0}^t (1 - \beta_i)\) and \(~\beta_t = \beta_{\text{end}} +\) \(\frac{t}{T - 1}(\beta_{\text{start}} - \beta_{\text{end}})\), and \(\sigma'_t = \mu\sigma_t, \mu=0.15\). While the standard self-diffusion loss relies solely on data fidelity, the joint estimation of \(\mathbf{x}\) and \(\mathbf{k}\) is a severely ill-posed problem that requires additional constraints. Therefore, we augment the loss with an \(\ell_1\) term for the kernel. The networks are jointly optimized within an inner loop by minimizing the following objective:

\begin{equation} \mathcal{L}_t(\theta, \phi) = | (D_\theta(\hat{\mathbf{x}}_t) \circledast G_\phi(\hat{\mathbf{z}}_t)) - \mathbf{y} |_2^2 + \lambda_k R(G_\phi(\hat{\mathbf{z}}_t)) \end{equation}

After the inner optimization loop, the improved networks produce cleaner estimates for the next time step, \(\mathbf{x}_{t-1} = D_\theta(\hat{\mathbf{x}}_t)\) and \(\mathbf{z}_{t-1} = G_\phi(\hat{\mathbf{z}}_t)\), continuing the coarse-to-fine reconstruction inherent to the self-diffusion process.

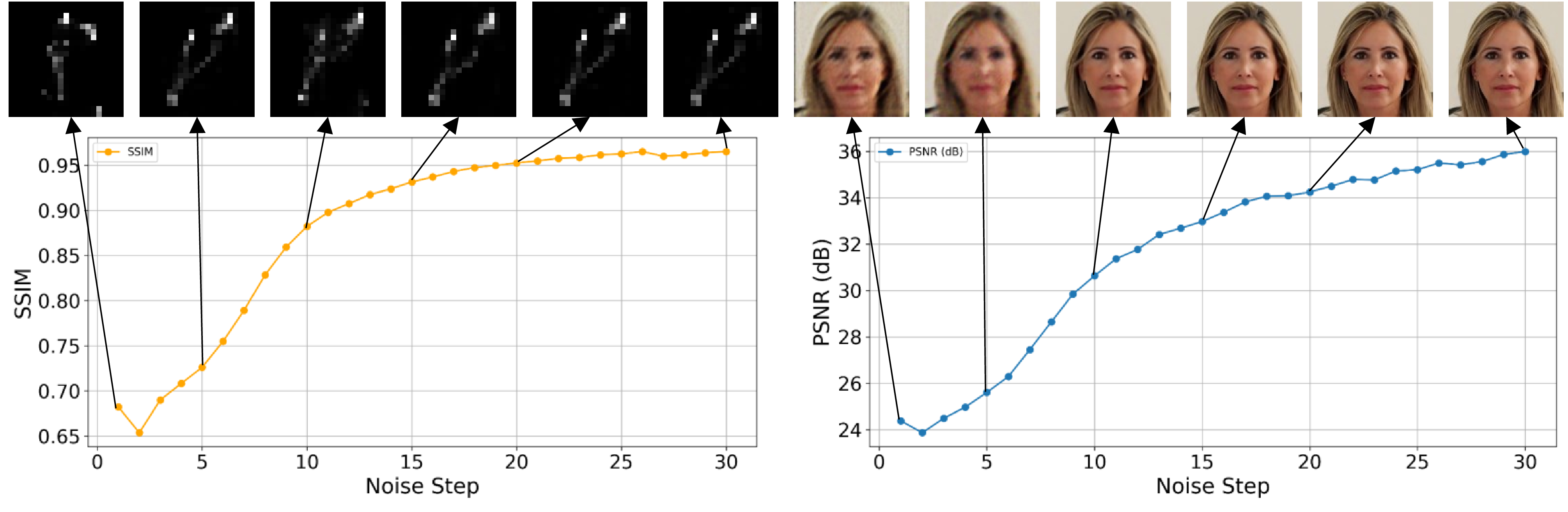
Results The following figure shows the evolution of estimates of image and kernel through the deblurring process. The left and right subfigures shows the SSIM and PSNR between the original image and the reconstruction over noise steps. The estimates of images and kernels at noise steps 5, 10, 15, 20, 30 are shown on the top. Unlike traditional optimization processes where evaluation metrics typically increase monotonically, our curves exhibit an up-down-up behavior (especially for PSNR curve), which is attributed to the noise scheduling strategy. By injecting noise into intermediate reconstruction results, we effectively enlarge the search space of the inverse solution. The initial reconstructions are smooth and lack fine detail, while later steps recover sharper features. This aligns with the coarse-to-fine nature of self-diffusion.

We compare our DeblurSDI method with several other blind deblurring approaches, including Phase-Only (Pan et al., 2019), FFT-ReLU Deblur (Al Radi et al., 2025), SelfDeblur (Ren et al., 2020), and FastDiffusionEM (Laroche et al., 2024).